Sound Extrapolation Method for Turbulent Flows
Siyang Zhong
Last updated on April 6, 2022
In computational aeroacoustics (CAA), the acoustic directivity patterns using the so-called hybrid methods. The near-field fluid/acoustic field is resolved using the high-accuracy numerical simulations while the sound extrapolation methods (or sometimes it is called sound projection methods) to account for the sound radiation processes.
Usually, the integral solution of the well-known Ffowcs-Williams and Hawkings (FW-H) equation (Proc. R. Soc. A., vol. 264, no. 1151, p. 321-342, 1969), which is one of the most important equations in the subject of aeroacoustics, is often employed for the hybrid computation. It is an exact rearrangement of the fluid governing equations, and it could provide the exact acoustic solution in case that the equation is exactly solved. However, in practical applications, the volume integral term is often omitted to save the computational expense and to avoid the difficulty of “cause-and-effect” issue (that unknowns appear in the source terms). One consequence of neglecting the volume terms is that the predicted sound field can be contaminated when the permeable integration surface is located in the turbulent flows. There were FW-H equation-based methods such as using on-body or open integration surfaces, which, however, have limitations in certain circumstances.
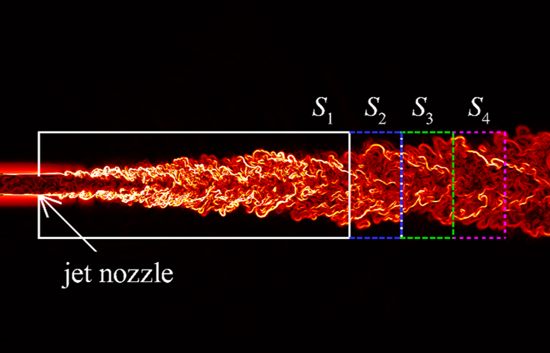
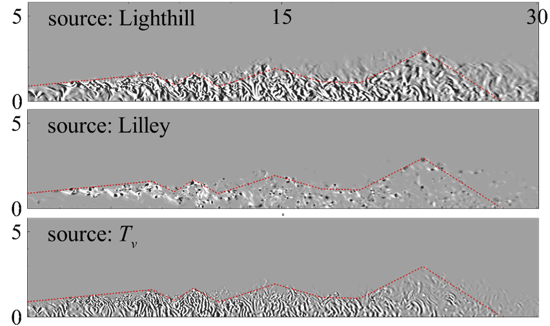
At AANTC, a series of studies were conducted to propose new sound projection methods that are suitable for turbulent flow applications. The key idea of the trend of studies is to filter out the non-acoustic (or acoustically inefficient) components in the turbulent flows before the various are employed for acoustic far-field computation. The idea is based on our understanding of that the turbulent flow fluctuations can be decomposed into the acoustical, vortical and entropy components (Kovasznay, J. Aero. Sci., vol. 20, no. 1 The initial study focused on filtering out the vortical components by developing a variant of the Lighthill’s acoustic analogy (Proc. R. Soc. A., vol. 211, p. 546-578, 1952), in which the mean flow is considered, and the fluctuations are defined based on the local mean flow components. In the source term, divergence and convection operators are acting on the velocity components such that the vortical velocities are filtered out. The method is suitable for the turbulent flow dominated by the vortical components, and it was applied to the airfoil-gust interaction problems, in both subsonic and transonic flows [1].
Reference
This work was supported by the Innovation and Technology Commission (Ref. ITS/038/FP15) and studentships from AVIC AANTC and HKUST.